I have a Substack now!

Hello everyone! I hope you all are doing well. This blog was my attempt to showcase my findings and others’ works that intrigued me during my high school math olympiad days. However, it’s been a while since I’ve moved passed that. I will be attending Emory University in the United States, and I think this blog will be unfortunately inactive until I’m up to some significant mathematical or scientific research in college.

BUT I have a Substack now! And I’m planning to write there more henceforth. Just yesterday I put out my Gap Year Journey post. So, feel free to connect with me on it, let me know your thoughts there, and check out my new website! Till then, see you and take care.

Posted on July 2, 2023 by Srijon Sarkar 0

My first paper – on ‘Midpoint of Symmedian Chord’!

I was so eager to share this. It is a paper on the so-called “Dumpty point“, which happens to be the midpoint of the respective symmedian chord. I had completed this in May itself, but then, I sent this to the Mathematical Reflections, and it took a bit of time (about 2 months, as they have their cycle of publishing issues), so, came late. But, anyway, finally, it’s up!

You can get a better formatted version here.

Comments, appreciations, or suggestions on my writing are absolutely and always more than welcome! Further, if you notice any errors/typos please put them here, no matter how trivial. Happy learning!

Join the community!

Posted on July 16, 2021February 2, 2022 by Srijon Sarkar 0

I found a lemma around the Mixtilinear Intouch point

This particular configuration turned out to be a trick for me. I came across it through this stream and ended up using it in a few problems, so thought to share. The very first problem, in which I noticed this can be found here. Later, I used it in the finish of IMO Shortlist 2014 G7, as you can see here. And lately, I again used it as a lemma in problem 13 of XVII I.F.Sharygin Geometry Olympiad’s CR. So, here goes the lemma.

Let $ABC$ be a triangle, with $I$ as the incenter. Let $D, Q$ denote the intouch & extouch point, respectively, on $\overline{BC}, M$ be the midpoint of $BC$ , and $T$ be the $A$ -Mixtilinear intouch point.
Further suppose, 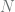$N$ is the midpoint of $AD$ , and take $D'$ to be the reflection of $D$ over $I$ , in other words, $D'$ to be the antipode of $D$ in $\odot(I)$ .

Property 1. $IM \parallel AQ$ .

Proof. We know that $BD = s-b = QC$ , i.e. $MD=MQ$ , and therefore, $M$ is the midpoint of $\overline{DQ}$ as well, yielding $NM \parallel AQ$ . Now, it’s well known that $A, D', Q$ are collinear, so by a homothety at $D$ with a ratio of $-\frac12$ we get $A, D', Q$ mapped to $N, I, M$ , respectively. Thus, $N, I, M$ are collinear, hence the desired; resulting in $\angle BMI = \angle BQA. \quad \square$

Property 2. $\angle BMI = \angle TCA$ .

Proof. It is well known that $AT$ and $AQ$ are isogonals. Now, we note that

$\angle BQA = \angle QAC + \angle QCA = \angle BCT + \angle BCA = \angle TCA$

as $\angle QAC = \angle BAT = \angle BCT$ , and we’re done. $\quad \square$

Remark. In the main context, some more points were considered, like $R$ to be the foot of the perpendicular from $B$ to $CT', R'$ as its reflection over $BC$ , and $T'$ as reflection of $T$ in $BC$ . But, those came inflow, while trying through the problem to get the solution; they aren’t needed, as can be noticed.

Comment. While the above comprises pretty much what I wanted to share, but note that, only these two didn’t finish any of the problems I mentioned; of course made a part of the job a little easier, but we had to do work before and after to get things done, accordingly.

About when you think to use this, maybe when you see the extouch point being there, and after some angle chase you get somewhere around $\angle QAC$ or so, you can consider this; now, as you have read through, you can catch that it’s a quite easy thing, especially the parallel part, maybe $\angle BMI = \angle BQA = \angle TCA$ is still worth it.

Warning: This is not at all a cite-able result, I believe; so, you should draw or outline the proof (in proper contests) if you solve or got through a problem by this; would hardly take few seconds; even if, this comprises a very small part of the solution, or is used most slightly.

Lastly, if you come across any other problem that you think can be solved by this or you already solved using this, or through any motivation from this, do let me know!

Update (June 3, 2021): So, Sharygin results came out on 28 of the last month, May, and it turned out that, my solution to p13 in which I used the above thing, is correct.

Update (July 28, 2021): See the use of property 1 one here (IMO Shortlist 2016 G2; in the first solution of the post); so, yea, another problem that uses this.

Join the community!

Posted on May 6, 2021February 2, 2022 by Srijon Sarkar 2

Euler’s Sum of Powers Conjecture

Many of you might know about Fermat’s Last Theorem, but very few know about Euler’s Sum of Powers Conjecture. It was conjectured in 1769 and it was disproved in 1966. It then went on to appear as a counter example in the 1989 AIME. Want to know more? Click here to download the article. (This post is very much inspired by the video of blackpenredpen; merely a verbatim article to share with you guys.)

Join the community!

Posted on April 9, 2020January 2, 2022 by Srijon Sarkar 1

Equally Equilateral

If the angles of a triangle are trisected, the intersections of the pairs of trisectors adjacent to the same side determine an equilateral triangle. This equilateral triangle is known as the first Morley triangle, or simply Morley’s triangle. (This is a generalization of Morley’s theorem, derived by Morley around 1900, and now it is known as the Morley’s Trisector Theorem.)

Comment 1. A more beautiful result can be obtained by taking the intersections of the exterior, as well as interior, angle trisectors. In addition to the first Morley triangle formed by the interior trisectors, four additional equilateral triangles are obtained, three of which have sides which are extensions of a central triangle.

Fermat points and Napoleon triangles

Given any $\triangle A B C$ , construct point $F_A$ such that $\triangle B F_A C$ is an equilateral triangle, with $F_A$ being on the opposite side of $BC$ as $A$ . Let $N_A$ be the circumcentre of $\triangle B F_A C$ . Similarly, define $N_B$ and $N_C$ . Now, join $N_A$ , $N_B$ , $N_C$ , to get $\triangle N_A N_B N_C$ . (Note that, the same construction applies to the other figure as well. Both the figures are exactly same, I’ve drawn two figures for better visualization.)

Given below, are few observations:

The circumcircles of the exterior triangles intersect at a common point $X$ .
The lines $A F_A$ , $B F_B$ and $C F_C$ also concur at point $X$ and are of the same length.
The point of concurrency, $X$ is known as the first Fermat point.
The circumcentres of the three equilateral triangles determine another equilateral triangle. This equilateral triangle is known as the outer Napoleon triangle.
The lines $A N_A$ , $B N_B$ and $C N_C$ are concurrent. This point of concurrency is called the first Napoleon point of $ABC$ .

Comment 2. If the equilateral triangles were erected internally on sides of the $\triangle A B C$ . Despite this, all the above properties would hold. But then, $\triangle N_A N_B N_C$ would be called the inner Napoleon triangle and the point $X$ would be called the second Fermat point. All these results holds even when $ABC$ is right-angled or obtuse-angled.

Note. For any point S in the plane of $\triangle A B C$ , consider the sum $S A$ + $S B$ + $S C$ . The point S for which the sum $S A$ + $S B$ + $S C$ is minimized, is none other than the point $X$ (same $X$ as above). The point $X$ is called the Fermat point of $\triangle A B C$ , or more generally the first Fermat-Torricelli point.

A Special Result

Suppose that $F$ is the Fermat point of $\triangle A B C$ . We can show that the nine-point centers – $N_1$ , $N_2$ , $N_3$ of the triangles $AFB$ , $BFC$ , $CFA$ respectively, form an equilateral triangle. Furthermore, $FX$ is a diameter of its circumcircle, where $X$ is the centroid of $ABC$ . Here, $F$ is the first Fermat point. The result holds for the second Fermat point as well. (This result was proved by my teacher, Aditya Ghosh.)

Join the community!

Posted on March 30, 2020February 2, 2022 by Srijon Sarkar 1

RSA Algorithm

There are two kids, Alice and Bob. Alice wants to send a message (M) to Bob, but they want to keep it confidential from others. If Alice tries to send that message via any route, then there are chances that a third person may intervene, and get the message. So, what do they do, to prevent it from happening? Click here to download the article.

Join the community!

Posted on March 27, 2020January 2, 2022 by Srijon Sarkar 1

Sierpinski Triangle

Do you know any figure which has an infinite perimeter but zero area? Isn’t it surprising? Click here to know more.

Join the community!

Posted on March 24, 2020January 2, 2022 by Srijon Sarkar 4

A Blog On Olympiad Mathematics